이번 포스팅에서는 공분산, 상관계수에 대해서 알아보겠습니다.
우선 공분산에 대해 알아보기 전, 일변량 분포의 분산에 대해 다시 한번 생각해봅시다.
X의 분산은 $Var(X) = E[(X-u)^2]$로 표현가능하며 평균에서 떨어진 값에 대한 제곱의 기댓값을 의미했었습니다.
즉, 평균에서 값들이 얼마나 벗어난지에 대한 측도로 생각할 수 있습니다.
공분산도 개념은 분산과 비슷한데요. 단지 일변량 함수의 개념에서 확장하여 두 개의 확률변수의 평균에서 벗어난 정도를 의미합니다.
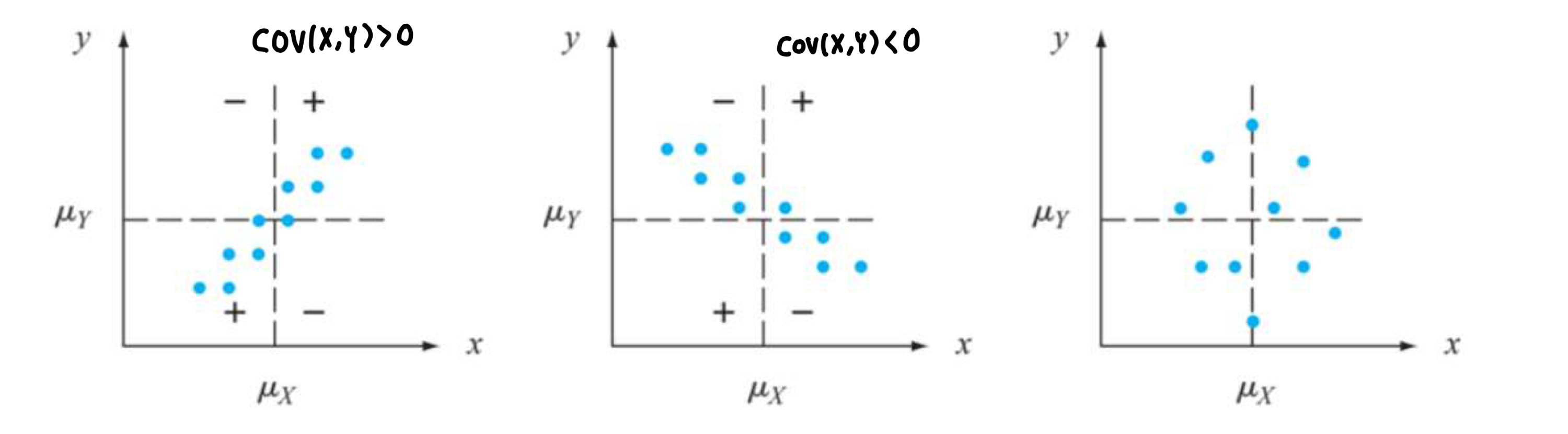
따라서, 식으로는 아래와 같이 나태날 수 있으며 두 확률변수 X, Y의 선형관계의 방향성을 나타내줍니다. 만약 공분산이 양수라면 두 확률변수의 관계가 양의 선형관계에 있으며 공분산이 음수라면 두 확률변수의 관계가 음의 선형관계에 있다고 말합니다.
(다만 대부분의 데이터 포인트가 양(음)의 선형관계가 있어도 일부 극단치의 관측치 때문에 음(양)의 선형관계가 있다고 나타날 수 있습니다.)
- Covariance : $Cov(X,Y) = E[(X-u_x)(Y-u_y)] = \sigma_{xy}$
- 이산확률변수의 Covariance : $\sum\sum(x-u_x)(y-u_y)f(x,y)$
- 연속확률변수의 Covariance : $\int\int(x-u_x)(y-u_y)f(x,y)dxdy$
이렇게 정의한 공분산의 특징은 아래와 같습니다. (단, a와 b는 실수)
- $Cov[a, X] = 0$
- $Cov[aX, bY] = abCov[X, Y]$
- $Cov[a+bX, c+dY] = bdCov[X, Y]$
- $Cov[X,X] = Var(X)$
- $Cov[X,Y] = E[XY] - E[X]E[Y]$
- X와 Y가 독립이라면 $Cov[X,Y]=0$ (단, 일반적으로 역은 성립하지 않으나 다변량 정규분포인 경우에는 역이 성립)
하지만 공분산의 단점으로는 변수의 측정 단위나 Scale에 의존하기 때문에 측정 단위가 다른 공분산과 비교하기에 어려움이 있습니다. 이런 단점을 해결하기 위해 상관계수가 나왔으며 공분산에서 각 확률변수의 표준편차를 나눠줌으로 구할 수 있습니다. 즉, 스케일링된 자료의 공분산을 구하는 것이므로 비교가 가능해지며 상관계수는 선형관계의 방향과 강도를 나타내게 됩니다. 공분산을 스케일링하기 위해서 고안된 만큼 선형변환을 하더라도 기존의 값과 동일하다는 특징을 가지고 있습니다.
(강도라고 해서 직선의 기울기가 크다는 의미가 아니라 직선 주위에 빽빽하게 모여있다는 뜻입니다.)
(+ 이번 포스팅에서는 Pearson 상관계수를 설명했는데 다양한 상관계수들이 존재합니다. https://moogie.tistory.com/145 )
- (Pearson Correlation) $Corr[X,Y] = \frac{Cov[X,Y]}{\sigma_X\sigma_Y} = \rho_{XY}$
- $Corr[a+bX, c+dY] = Corr[X,Y]$
저는 학부시절에 $E(XY)$가 두 확률변수의 기댓값의 곱과 왜 다를까 생각했었습니다.
멘토링을 하면서 많은 친구들도 헷갈려하는데 이는 공분산과 상관계수의 특징에 따라 다음을 유도할 수 있습니다.
공분산 5번째 특징에 따라, $E[XY] = Cov[X,Y] + E[X]E[Y]$이며 상관계수의 정의에 따라 다음과 같이 나타낼 수 있습니다.
$$E[XY] = E[X]E[Y] + \rho_{XY}\sigma_X\sigma_Y$$
즉, 두 확률변수의 곱의 기댓값($E[XY]$)은 두 확률변수의 기댓값의 곱에 표준편차와 상관계수를 사용해 표현할 수 있습니다.
'Statistics > Mathmetical Statistics' 카테고리의 다른 글
| [확률과 통계적 추론] 4-3.1 조건부분포와 상관계수의 관계 (2) | 2024.01.03 |
|---|---|
| [확률과 통계적 추론] 4-3. 조건부 분포 (Conditional Distribution) (3) | 2024.01.03 |
| [확률과 통계적 추론] 4-1. Bivariate Distribution (이변량분포) (0) | 2023.07.30 |
| [확률과 통계적 추론] 3-5. 혼합타입분포(Mixed Type Distribution) (0) | 2023.05.21 |
| [확률과 통계적 추론] 3-4. Failure Rate(고장율) (2) | 2023.05.21 |